Zero-knowledge Proof Part 1

STACK-X Webinar — Introduction to Zero-knowledge Proof (Part 1)

The following article was adapted from a STACK-X Webinar conducted by Raymond Yeh, a software engineer at GovTech, on June 25, 2020.

This is the first post of a two-part series on Zero-knowledge Proofs.

 

What’s a Zero-knowledge Proof (ZKP)?

You may or may not have heard the term before, but a ZKP is essentially a method of proving that one has knowledge of something without sharing the contents of one’s knowledge. The possible applications of such a proof have, in more recent years, garnered much attention, especially with regards to solving privacy-related issues.

But maybe that’s all a little abstract.

To help you better understand what ZKPs are and what they would even look like, here’s a scenario for you to think about (adapted from The Startup’s article):

A simple game of Where’s Waldo

Both you and a friend have been asked to solve a Where’s Waldo puzzle. In front of you is a printout of an illustration filled with hundreds of people (including Waldo, of course).

Being keen-eyed, it’s not long before you locate Waldo. Your friend, however, is having a far harder time with this. When you tell him that you’ve already found Waldo, he naturally doesn’t believe you—not only that, he even asks you to prove it.

Herein lies the problem: you want to show him that you know where Waldo is without showing him Waldo’s location so that he can continue to try and solve the puzzle on his own (or maybe you just want to watch him struggle a bit more).

The proof we’re describing here is—you guessed it—a ZKP. So, what would that look like for this problem?

Here’s a possible answer:

To begin with, get a very large piece of cardboard (say, four times the size of the puzzle) and choose a place to cut out the outline of Waldo. Then, place it over the Where’s Waldo illustration so that your friend can see only Waldo and nothing else. Without being able to see the rest of the illustration behind the cardboard, your friend won’t be able to tell which part of the picture Waldo is in, but he’ll be able to see that you really do know where Waldo is.

With that, you’ve proven to your friend that you know the solution to this puzzle without ever revealing said solution—you’ve created a ZKP!

What are some real-world applications of ZKP?

So, now you know what a ZKP is. But let’s be honest—how often are we going to find ourselves in a Where’s Waldo scenario like the one we just saw? For that matter, are there really many situations where a ZKP can come in handy?

…Definitely!

Here’s just one example (that we’ll actually be creating a ZKP for if you read on): imagine that you want to prove that you’re over the legal age limit when buying alcohol at a grocery store. However, your age is a very sensitive piece of information that you’d really rather not reveal. Creating a ZKP would allow you to prove to the cashier that you’re over the legal age without ever specifying your exact age.

There are, of course, many other useful applications for ZKPs, such as:

Anonymous Verifiable Voting – proving that one has the right to cast a vote (they have citizenship, for instance), that the vote has been included and also that the vote tally is correct—all without revealing anything about the identity of voters.

Accountancy – proving that the computation of a balance sheet is correct without showing the actual items on the sheet.

Solvency – proving that a financial institute has sufficient reserves to settle at least x% of accounts without revealing the sum of their reserves.

If you’re interested in the full range of potential applications for ZKPs, you can check out this research paper in your spare time.

But moving on to the overview of the ZKP landscape today…

 The world of ZKPs

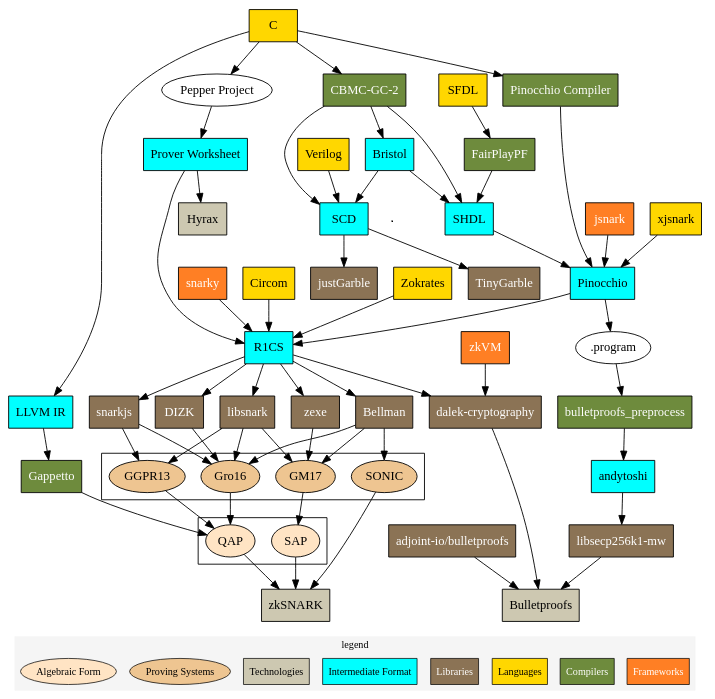
This overview of the current ZKP landscape may seem intimidating, but fret not! We’ll walk you through the important bits.

The yellow boxes (C, SFDL, etc.) represent the various programming languages you can write ZKP circuits in.

In the grey boxes, you can see two widely known technologies that make use of ZKPs: zk-SNARKs and Bulletproofs.

The term zkSNARK is actually an acronym that stands for:

Zero-knowledge – does not reveal contents of knowledge.

Succinct – the proof can be verified within a few milliseconds and the proof length is only a few hundred bytes.

Non-interactive – a single message is sent from the prover to the verifier rather than a series of communications.

Argument of knowledge – a computationally sound proof.

In Part 2 of this series, we’ll be focusing on zk-SNARKs and writing a ZKP using ZoKrates.   

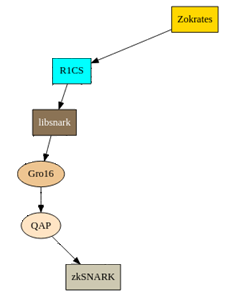
Following this snippet of the larger chart above, you’ll see that the code we’ll be writing (using ZoKrates) will be automatically compiled to R1CS, and then libsnark, Gro16, QAP and finally zk-SNARKs.

(If you’re well-versed in RSA maths and want a deeper dive into the construction of zk-SNARKs, check out this Medium article after you’re done here.)

Now, hopefully you’ve remembered the legal age restriction scenario we briefly talked about, because next we’ll be looking at a demo application of this age-restriction ZKP.

Demo time!

The goal is to construct a ZKP that will prove to our check-out cashier that we are indeed above the age limit (let’s take this to be 21 here). This could take the simple form of an application on their screen—the cashier would input the relevant values into several boxes and the application would return a true or false verification.

Now, when we talk about building a ZKP here, what we’re really talking about is building a ZKP Circuit (i.e. the grey box below).

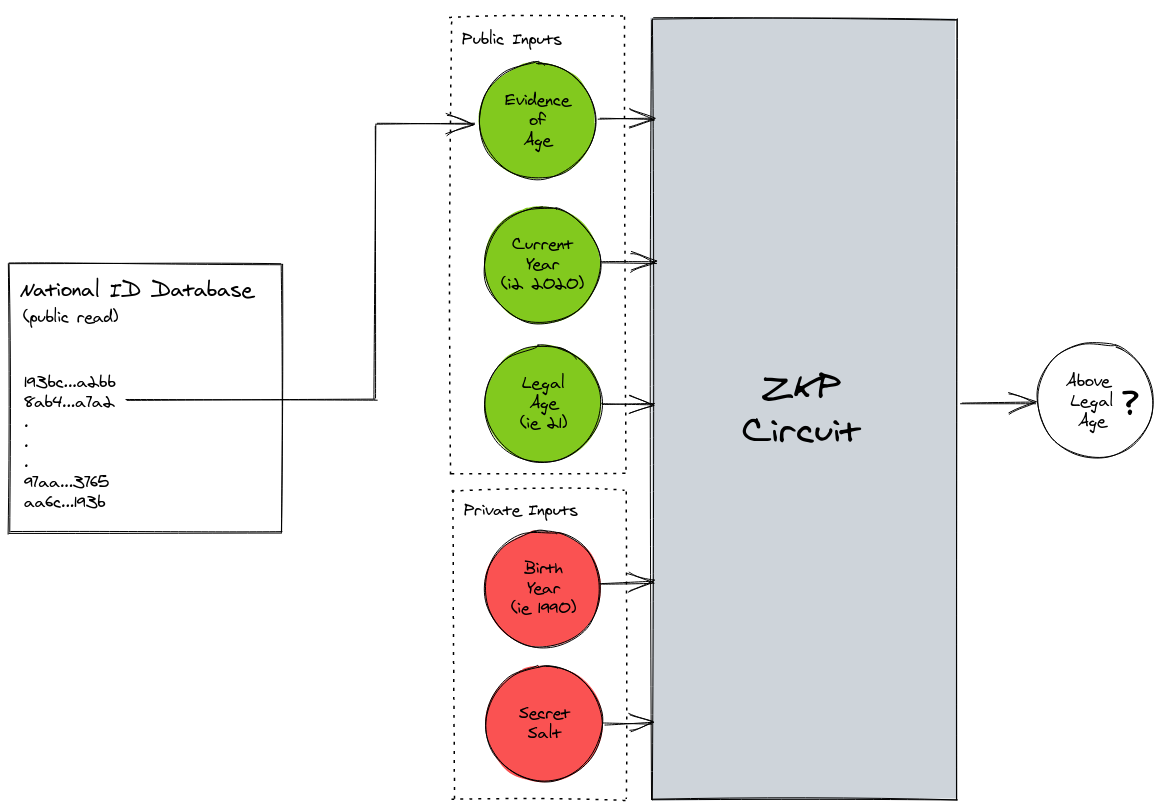
We’ll crack open this box and see how it works in a short while, but for now, let’s examine the inputs that go into this circuit.

Firstly, our public inputs. These are pieces of information that allow our cashier to verify that the business constraint ‘above 21 years old’ holds even though they don’t have knowledge of our private inputs—secret information that is never presented to the cashier.

Public inputs:

Evidence of age – Official documentation that verifies our birth year. For our purposes, let’s take it that this evidence comes in the form of a hash. This hash is created from our birth year and a secret salt (more on this in a bit).

• Side note: If you’re not familiar with hashing, it’s a one-way function that converts a key (this could be anything, including a word or, in our case, a number) into a random string of characters (the hash). This process cannot be reversed, so the original value will be difficult to uncover. Think of it like baking a cake—you can take a variety of ingredients and bake them into a cake, but you can’t reverse the process and un-bake the cake to retrieve the ingredients.

Current year – Our cashier needs to compare this with the evidence of our age and the legal drinking age to determine if we’re over the age limit.

Legal drinking age – Likewise, this is needed to confirm that we’re of age.

Next, our private inputs:

Birth year – We need this to prove that we’re over 21!

Secret salt – In hashing, adding a salt means adding an additional input. In this case, instead of just inputting the year 1990 (for example) to be hashed, we might add the string of characters ‘fla19297dnag54’ alongside it to derive a stronger hash. This is necessary because without it:

• Attackers can attempt to enumerate a series of possible birth years (running years like 1980-2000 through a hash function) and compare the resultant hashes with the hash created from only our birth year. The moment they notice that one of the hashes is identical with our hash, they’ll know what our age is.

• It is possible for two individuals to have the same official hash if their birth years are the same. If you saw someone else with the same hash, you’d immediately know their age.

Now that we understand our inputs, it’s time to take a look inside our grey box:

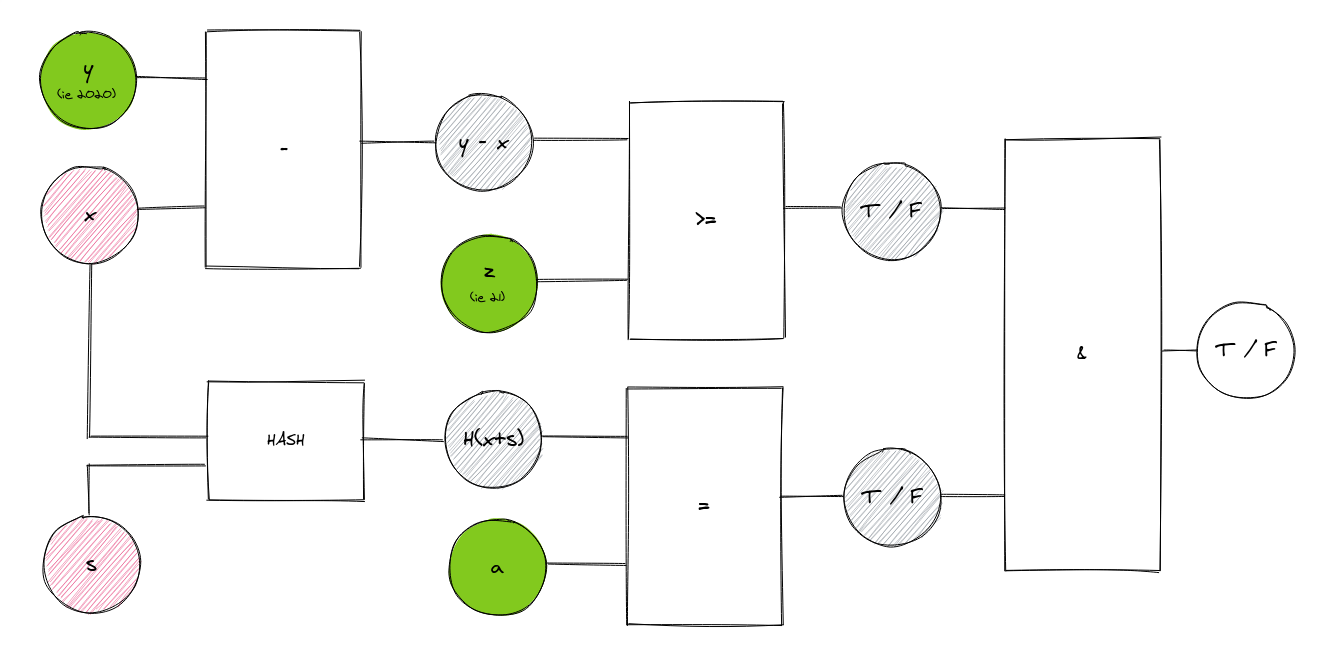
You can see that our various inputs are in this circuit, with red and green corresponding to our private and public inputs as per the previous chart. Our birth year (x) is inputted along with a secret salt (s) to form our hash (H). This is then cross-checked with our evidence of age (a). If H’s value matches a’s, we get a true signal (T).

At the same time, the current year (y) is subtracted from x. The resulting number is then compared with the legal drinking age (z). If it is greater than or equal to z, we get T.

If both constraints hold, it is determined that we are indeed of legal age, which results in the system verifying this as true.

And there you have it!

Some final remarks

• ZKPs are proofs of knowledge that can be useful in keeping sensitive information private.

• A circuit is useless without external data or constraints, as it’s simply a proof of knowledge. A ZKP circuit needs business constraints in order to form an application.

• Take note—ZKPs are not blockchains! ZKPs are heavily used in the blockchains, but they’re not one and the same.

• ZKPs are great, but they’re not a panacea for every privacy-related problem. As with most things, it depends on the situation.

That’s all for Part 1 of our STACK-X Introduction to Zero-knowledge Proofs, but now that we’ve gotten you up to speed on what ZKPs are, you’re ready to try your hand at writing a ZKP application! For that, you can head over to Part 2.

 

By Raymond Yeh and Michael Tan

Published on 22 July 2020.

Last updated 28 February 2023

---